D3 נוסחת טאפר, קנה מידה ו

נתקלתי בפוסט הכיפי של גדי אלכסנדרוביץ’ על נוסחת טאפר והחלטתי שכדאי לראות מה אפשר לעשות איתו ב D3.

בקיצור נמרץ, הפוסט מספר על נוסחה לפענוח קידודים של תמונות מונוכרומטיות והדוגמא הניתנת היא הקוד שמכיל את הנוסחה עצמה.

הקוד הבא (k פורק לשורות בשביל הנראות – בקוד האמיתי הוא מחרוזת רצופה):

<script src="js/big.min.js"></script>
<script>
    var k = new Big("9609393799189588849716729621278527547150043396601293
                     0665150551927170280239526642468964284217435071812126
                     7153782770623355993237280874144307891325963941337723
                     4878577357498239266297155171737169951652328905382216
                     1240323885586618401323558513604882869333790249145422
                     9288667081096184496091705183454067827731551705405381
                     6273809676025656250169814820834187831638491155902256
                     1000365235137034387446184837873723819822484986346503
                     3159410054974700593138339226497249461751545728366702
                     3697454610146559979337985374831437868418065934222278
                     98388722980000748404719");
    var data = [];

    //איכלוס המערך - בכל מקום שאי השיוויון מתקיים, מוסיפים את הקואורדינטה
    k = k.div(17);
    for (var x = 105; x >= 0; x = x - 1) {
        for (var y = 0; y < 17; y++) {
            var bit = floor(k.mod(2));
            if (bit == 1)
                data.push({x: x + 1, y: y + 1});
            k = floor(k.div(2));
        }
    }

    var svg = d3.select("#tupper").append("svg")
            .attr("width", 120)
            .attr("height", 20);

    //וכמו בפוסט הקודם - מזינים את המערך ולכל פריט בו מציירים עיגול קטן
    svg.selectAll("circle")
            .data(data)
            .enter().append("circle")
            .attr("cx", function (d) {return d.x;})
            .attr("cy", function (d) {return d.y;})
            .attr("r", 1)
            .attr("fill", "black");

    function floor(bd){
        return bd.round(0, 0);
    }
</script>

 

מייצר את הנוסחה מהקידוד שלה:

האמת היא, שלא כ"כ רואים, הנוסחה מצוירת על מלבן של 105x17 פיקסלים והרדיוס של העיגולים הוא 1. אנו רוצים להגדיל את התמונה ולשם כך נעזר בפונקציונליות של d3 שנקראת scale.

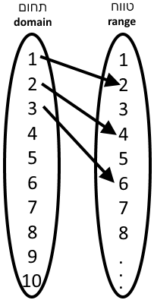
סקאלות (scales) הן אוסף של פונקציות הממפות אוסף של ערכי קלט לאוסף של ערכי פלט. הקלט נקרא תחום (domain), והפלט נקרא טווח (range). סקאלות יכולות למפות סוגים שונים של נתונים: מספרים למספרים, תאריכים לצבעים וכו'.

דוגמא פשוטה תהיה פונקציה שהתחום שלה הוא [1-10] והטווח שלה הוא [1-20] והמיפוי הוא בין מספר למכפלה שלו ב 2. הציור הבא ממחיש זאת:

 

כיצד נוכל להשתמש בסקאלות כדי לראות את נוסחת טאפר טוב יותר?

נתמקד כרגע בסקאלות ליניאריות (כמו פונקציה ליניארית מהסוג: y = mx + b) שמאפשרות מיפוי נח בין קלטים ופלטים רציפים. בדוגמא שלנו נרצה שכל מעגל יהיה ברדיוס גדול מ-1. ע"מ לאפשר זאת נצטרך לשנות את הקואורדינטות של הנק' שלנו. נבנה ראשית את סקאלת ה X:

var scale = 5;
var scaleX = d3.scale.linear()
        .domain(d3.extent(data, function(d){return d.x;}))
        .range([
            d3.min(data, function(d){return d.x;}) * scale,
            d3.max(data, function(d){return d.x;}) * scale
        ]);

המשתנה scaleX הוא פונקציה שהנתונים שלה הן הנק' (המשתנה data), התחום שלה הוא רציף בין ה X המינימלי ל X המקסימלי והטווח שלה הוא בין ה X המינימלי ל X המקסימלי אבל במכפלה של 5. כלומר עבור נק' שבה x=1 נקבל עכשיו x=5, עבור x=3 נקבל x = 15 וכך הלאה.

נבנה גם סקאלה עבור ציר ה Y:

var scaleY = d3.scale.linear()
        .domain(d3.extent(data, function(d){return d.y;}))
        .range([
            d3.min(data, function(d){return d.y;}) * scale,
            d3.max(data, function(d){return d.y;}) * scale
        ]);

נבנה כעת את המשוואה ונשתמש בסקאלות שיצרנו:

svg.selectAll("circle")
        .data(data)
        .enter().append("circle")
        .attr("cx", function (d) {return scaleX(d.x);})
        .attr("cy", function (d) {return scaleY(d.y);})
        .attr("r", scale - 1) // =4
        .attr("fill", "black");

וכעת נקבל:

יש סקאלות נוספות שנועדו לתת מענה לנתונים שמיוצגים אחרת (למשל נתונים בדידים). צריך לזכור שהרעיון המרכזי הוא זה: מיפוי בין אוסף ערכים לאוסף אחר של ערכים. מכאן השמיים הם הגבול...

לקראת הפוסט הבא שבו נראה דרך נוספת להגדיל את התמונה (והרבה יותר קצרה במונחים של קוד), אל תעבירו את העכבר מעל המשוואה הבאה:

קריאה נוספת:

https://github.com/mbostock/d3/wiki/Quantitative-Scales